Rattenrace - reken rdzl
|
Op de kermis kun je net zo vaak als je wilt meedoen met het spel "rattenrace". In dat spel wordt een rat losgelaten aan het begin van een parcours. De rat rent dan naar poortje A, B of C, ieder met evenveel kans. Je kunt van te voren ieder bedrag dat je wilt, inzetten op het poortje waar de rat in zal gaan. Als je het goed hebt, krijg je het dubbele bedrag terug, als je verkeerd hebt gegokt, verlies je je geld. Neem aan dat je oneindig veel geld bij je hebt. Verlies je dan uiteindelijk altijd geld met dit spel of is er een tactiek te bedenken waarmee je zeker winst kan maken? En wat in de meer realistische situatie als je een eindige hoeveelheid geld bij je hebt? Of als er een maximum inzet is? |

|
Uitleg
De kans dat de rat door poortje A, B of C gaat is natuurlijk 1/3. Maar dit is eigenlijk helemaal niet zo belangrijk, als je altijd maar inzet op poortje A, zul je ooit wel een keer iets winnen.
Nu de tactiek, zet eerst 1 euro in op poortje A, als je verliest ben je 1 euro kwijt, als je het goed hebt heb je 1 euro gewonnen.
Als je verloren hebt zet je het dubbele bedrag, 2 euro in op poortje A. Dat kun je natuurlijk weer verliezen, dan heb je in totaal 3 euro verloren. Als je wint heb je in totaal 1 euro gewonnen.
Je moet net zolang blijven verdubbelen, todat de rat een keer door poortje A gaat, en dan stoppen. Dan heb je uiteindelijk 1 euro verdiend.
Door steeds het ingezette bedrag te verdubbelen, krijg je bij winst al het verloren geld weer terug.
Maar het kan nog veel mooier, als je durft. Dan moet je gewoon iedere keer het bedrag verdrievoudigen of nog meer vergroten. Als je begint met 1 euro en je ver-N-voudigd het ingezette bedrag iedere keer dan win je als de rat pas in de n-de beurt door poortje A gaat
N^(n-1) - (1 + N + N^2 + N^3 + N^(n-2)) = (N^n - 2 N^(n-1) + 1)/(N-1) euro's.
Stel je begint met een euro, je verviervoudigd iedere keer je inzet en na 6 beurten gaat de rat door poortje A. Je hebt dan 683 euro verdiend!
Maar dit is theorie. In het echt ga je natuurlijk niet met oneindig veel geld naar de kermis. Daarom kun je op een gegeven moment je inzet niet meer ver-N-voudigen. Dat gebeurt natuurlijk ook als er een bovengrens op de inzet bestaat.
Neem aan dat er niet zo'n bovengrens bestaat, en dat je x euro's bij je hebt. The kans p dat je goed gokt is elke ronde 1/3. De inzet ver-N-voudig je iedere keer. Als je wint krijg je M keer je inzet terug (M = 2) in dit geval.
Omdat je x euro's bij je hebt kan je maar een eindig aantal ronden spelen. Als je iedere ronde ver-N-voudig vanaf 1 euro, en n ronden moet spelen totdat je wint heb je
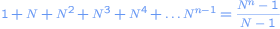
euro's nodig. Het aantal ronden dat je maximaal kunt spelen is dus het grootste getal n waarvoor geldt dat
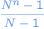
kleiner is dan x.
Nu kunnen we de volgende tabel maken
De kans dat je niet wint in de n-de ronde en moet stoppen is (1-p)^n. In dat geval verlies je (N^n - 1)/(N-1) euro's.
Nu kunnen we de verwachtingswaarde S bepalen van de te verwachten opbrengst. Dat is de kans dat je wint in de eerste ronde keer keer de opbrengst in de eerste ronde + de kans dat je wint in de tweede ronde keer de winst in de tweede ronde + .... + de kans dat je wint in de n-de ronde keer de winst in de n-de ronde - kans dat je verliest in de n-de ronde keer het totale verlies.
Uit de tabel volgt dat
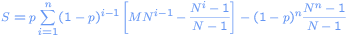
De voorgaande formule kan vereenvoudigd worden tot
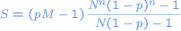
Als p * M kleiner is dan 1, is het te verwachten dat je geld zal verliezen met deze tactiek. p * M is natuurlijk kleiner dan 1 in ieder realistisch spel (je krijgt natuurlijk niet 3 keer je inzet terug als de kans om te winnen 1/2 is). In het rattenrace spel is p * M = 2/3 = 0.666666. Je verliest dus uiteindelijk altijd met het rattenrace spel omdat je maar een eindige hoeveelheid geld kan nemen. De ver-N-voudigingstechniek werkt dus niet in een realistische situatie.
Nu de tactiek, zet eerst 1 euro in op poortje A, als je verliest ben je 1 euro kwijt, als je het goed hebt heb je 1 euro gewonnen.
Als je verloren hebt zet je het dubbele bedrag, 2 euro in op poortje A. Dat kun je natuurlijk weer verliezen, dan heb je in totaal 3 euro verloren. Als je wint heb je in totaal 1 euro gewonnen.
Je moet net zolang blijven verdubbelen, todat de rat een keer door poortje A gaat, en dan stoppen. Dan heb je uiteindelijk 1 euro verdiend.
Door steeds het ingezette bedrag te verdubbelen, krijg je bij winst al het verloren geld weer terug.
Maar het kan nog veel mooier, als je durft. Dan moet je gewoon iedere keer het bedrag verdrievoudigen of nog meer vergroten. Als je begint met 1 euro en je ver-N-voudigd het ingezette bedrag iedere keer dan win je als de rat pas in de n-de beurt door poortje A gaat
N^(n-1) - (1 + N + N^2 + N^3 + N^(n-2)) = (N^n - 2 N^(n-1) + 1)/(N-1) euro's.
Stel je begint met een euro, je verviervoudigd iedere keer je inzet en na 6 beurten gaat de rat door poortje A. Je hebt dan 683 euro verdiend!
Maar dit is theorie. In het echt ga je natuurlijk niet met oneindig veel geld naar de kermis. Daarom kun je op een gegeven moment je inzet niet meer ver-N-voudigen. Dat gebeurt natuurlijk ook als er een bovengrens op de inzet bestaat.
Neem aan dat er niet zo'n bovengrens bestaat, en dat je x euro's bij je hebt. The kans p dat je goed gokt is elke ronde 1/3. De inzet ver-N-voudig je iedere keer. Als je wint krijg je M keer je inzet terug (M = 2) in dit geval.
Omdat je x euro's bij je hebt kan je maar een eindig aantal ronden spelen. Als je iedere ronde ver-N-voudig vanaf 1 euro, en n ronden moet spelen totdat je wint heb je
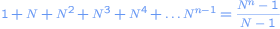
euro's nodig. Het aantal ronden dat je maximaal kunt spelen is dus het grootste getal n waarvoor geldt dat
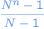
kleiner is dan x.
Nu kunnen we de volgende tabel maken
| Ronde | Inzet | Kans op goede gok | Winst als je goed gegokt hebt | 1 | 1 | p | M - 1 |
| 2 | N | p(1-p) | M*N - N - 1 |
| 3 | N*N | p(1-p)^2 | M*N^2 - N^2 - N - 1 |
| .. | .. | .. | .. |
| n | N^(n-1) | p(1-p)^(n-1) | M * N^(n-1) - (N^n - 1) / (N - 1) |
Nu kunnen we de verwachtingswaarde S bepalen van de te verwachten opbrengst. Dat is de kans dat je wint in de eerste ronde keer keer de opbrengst in de eerste ronde + de kans dat je wint in de tweede ronde keer de winst in de tweede ronde + .... + de kans dat je wint in de n-de ronde keer de winst in de n-de ronde - kans dat je verliest in de n-de ronde keer het totale verlies.
Uit de tabel volgt dat
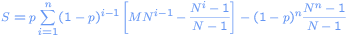
De voorgaande formule kan vereenvoudigd worden tot
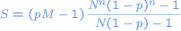
Als p * M kleiner is dan 1, is het te verwachten dat je geld zal verliezen met deze tactiek. p * M is natuurlijk kleiner dan 1 in ieder realistisch spel (je krijgt natuurlijk niet 3 keer je inzet terug als de kans om te winnen 1/2 is). In het rattenrace spel is p * M = 2/3 = 0.666666. Je verliest dus uiteindelijk altijd met het rattenrace spel omdat je maar een eindige hoeveelheid geld kan nemen. De ver-N-voudigingstechniek werkt dus niet in een realistische situatie.
|
|