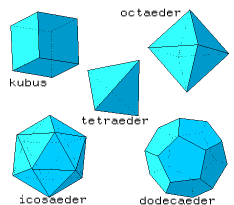
Laat zien dat er maar vijf platonische lichamen bestaan (dat zijn regelmatige veelvlakken, zoals de tetraeder en de kubus). Hint: gebruik dat voor ieder veelvlak in drie dimensies geldt dat het aantal hoeken + het aantal vlakken gelijk is aan het aantal ribben plus twee.

Noem het aantal hoeken van een veelvlak H, het aantal vlakken V en het aantal ribben (zijden) N. Er geldt dat H + V = N + 2.
Een regelmatig veelvlak is opgebouwd uit gelijkzijdige polygonen. Het aantal polygonen is dus gelijk aan V. Noem het aantal zijden van zo'n polygon n.
In ieder hoekpunt van een regelmatig veel vlak komen een gelijk aantal ribben samen, noem dit aantal m. Een tetraeder is bijvoorbeeld opgebouwd uit vier gelijkzijdige driehoeken en in ieder hoekpunt komen 3 lijnen samen, dus dan V = 4, m = 3 en n = 3.

Nu geldt dat het aantal ribben gelijk is aan het aantal vlakken maal het aantal zijden van het polygon gedeeld door twee (iedere ribbe is een zijde van twee polygonen). Dus
N = V * n / 2
Het aantal hoeken is gelijk aan het aantal ribben gedeeld door m / 2, dus
H = 2 * N / m
Gebruikmakend van H + V = N + 2 vinden we dat
2 * N / m + 2 * N / n = N + 2
oftewel
1/N = 1/m + 1/n - 1/2.

Eerst bekijken we alle mogelijke veelvlakken opgebouwd uit gelijkzijdige driehoeken, dus met n = 3. Met behulp van de bovenstaande formule vinden we dat
1/N = 1/m - 1/6
Deze vergelijking heeft de volgende oplossingen:
m = 3, N = 3. Hieruit volgt H = 3 en V = 3. Dit is een tetraeder.
m = 4, N = 12. Hieruit volgt H = 6 en V = 8. Dit is een octaeder.
m = 5, N = 30. Hieruit volgt H = 20 en V = 20. Dit is een icosaeder.
Voor m groter dan 5 heeft de vergelijking geen oplossingen omdat het rechter deel dan nul of kleiner dan nul wordt, terwijl het linkerdeel altijd positief is. Er bestaan dus 3 regelmatige veelvlakken opgebouwd uit gelijkzijdige driehoeken.

Nu het aantal mogelijke regelmatige veelvlakken opgebouwd uit gelijkzijdige rechthoeken. Dan hebben we n = 4 en de formule
1/N = 1/m - 1/4.
Deze vergelijking heeft de volgende oplossing
m = 3, N = 12. Hieruit volgt H = 8 en V = 6. Dit is een kubus. Voor m groter dan 4 heeft de vergelijking geen oplossingen. Dus er is een regelmatig veelvlak opgebouwd uit gelijkzijdige rechthoeken.

Nu het aantal mogelijkheden met n = 5. Dan geldt
1/N = 1/m - 3/10
De enige oplossing van deze vergelijking is
m = 3, N = 30. Hieruit volgt dat H = 20 en V = 12. Dit is een dodecaeder.

Voor n groter dan 5 heeft de formule 1/N = 1/m + 1/n - 1/2 geen oplossingen. Dit komt omdat in dat geval 1/m + 1/n - 1/2 altijd kleiner is dan nul. Er bestaan dus geen regelmatige veelvlakken opgebouwd uit gelijkzijdige n-hoeken met n groter dan 5.

Nu hebben we aangetoond dat er vijf platonische lichamen bestaan, de tetraeder, de kubus, de octaeder, de dodecaeeder en de icosaeeder.