Pijpleiding - reken rdzl
| Een offshore bedrijf wil op de goedkoopste manier een pijpleiding aan laten leggen vanaf een punt aan de kust naar een boorplatform in zee (zie het kaartje hiernaast, het beginpunt is het zwarte vakje, het rode rondje stelt het boorplatform voor). De kust (met strand) is in dit stuk helemaal recht, zoals op het kaartje te zien is. Het boorplatform ligt 6 km uit de kust en de afstand van het boorplatform tot het beginpunt is 10 km. Het aanleggen van een rechte pijpleiding langs het strand kost 0,3 miljoen euro per kilometer, door zee kost het 0,5 miljoen euro per kilometer (onafhankelijk van de diepte). Hoeveel moet het offshore bedrijf voor het aanleggen gaan betalen? |

|
Uitleg
Er zijn twee manieren om dit probleem op te lossen, de eerste is de wiskundige aanpak, de tweede de natuurkundige (die wiskundig gezien eenvoudiger is, met dank aan H. Lichtenberg). Allereerst behandelen we de wiskundige aanpak. Daarna bekijken we hoe we dit probleem op een natuurkundige manier kunnen oplossen.
De wiskundige aanpak
De beste manier om de pijpleiding is om eerst een stuk langs het strand aan te leggen en dan recht door zee naar het boorplatform. Om de goedkoopste oplossing te bepalen moeten we de totale kosten minimaliseren. Noem de totale kosten van het aanleggen K miljoen euro. De kosten voor het aanleggen langs het strand noemen we S miljoen euro per kilometer, door zee Z. De afstand (in km) van het boorplatform tot het strand noemen we y, die van het beginpunt tot het boorplatform d, en die van het beginpunt tot het punt op het strand recht tegenover het boorplatform x. De lengte van de pijpleiding langs het strand noemen we a en die door zee noemen we b.
Er geldt dus dat
K = a S + b Z.
en met de stelling van Pythagoras (sqrt = wortel)
b = sqrt(y^2 + (x - a)^2).
Dus de totale kosten zijn
K = a S + sqrt(y^2 + (x - a)^2) Z.
De minmimale kosten kun je vinden door K te differentieren naar a en gelijk aan nul te stellen. Dat geeft
S + (x - a) / (sqrt(y^2 + (x-a)^2) * Z = 0.
Werken we de bovenstaande vergelijking verder uit dan vinden we
(x - a)^2 = S^2 y^2 / (Z^2 - S^2).
a = x - S y / sqrt(Z^2 - S^2) (hier gebruiken we dat Z groter is dan S).
Nu kunnen we het resultaat voor a invullen in de eerste formule. We vinden dan dat de minimale kosten gelijk zijn aan
K = x S + y * sqrt(Z^2 - S^2).
Nu is x gelijk aan 8 km (sqrt(10*10 - 6*6)), y gelijk aan 6 km, S is 0,3 miljoen euro per km, en Z is 0,5 miljoen euro per kilometer. Vullen we alles in dan vinden we dat K = 2,4 + 2,4 = 4,8 miljoen euro.
Het aanleggen van de pijpleiding op de goedkoopste manier kost dus 4,8 miljoen euro.
De natuurkundige aanpak
Voor het probleem van het boorplatform is een ook een veel eenvoudiger oplossing. Tenminste, als je de stap durft wagen om het vraagstuk om te zetten in een natuurkundig probleem.
We veranderen ÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂgeldÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂ in ÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂtijdsduurÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂ en passen het probleem aan. Het gaat er nu om de afstand tussen A en B in zo weinig mogelijk tijd af te leggen. Langs het strand gaat met 0,3 s per km (snelheid v1 = 3,33 km/s), door zee gaat het met 0,5 s per km (snelheid v2 = 2 km/s). En wat is nu meer geschikt op dit vraagstuk op te lossen dan een lichtstraal (die immers altijd de kortste weg in tijd kiest)? Zie hier onder een schets van de situatie.
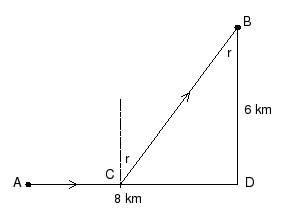
De straal gaat van A naar C en wordt gebroken naar B. Bij C is de invalshoek i = 90 graden, de brekingshoek is r. Volgens de brekingswet van Snellius is:
sin 90/sin r = v1/v2, dus: sin r = v2/v1 = 0,6.
Dan moet r = 36,9 graden en dus tan r = 0,75.
Dan volgt: CD = 4,5 km en AC = 3,5 km (want AD = 8 km). Verder is CB = 7,5 km.
De tijd voor AC is dus 3,5 x 0,3 = 1,05 s; de tijd voor CB is 7,5 x 0,5 = 3,75 s.
Totaal is dat 4,8 s.
Nu volgt de ÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂterugvertalingÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂ naar miljoenen euroÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂs.
De wiskundige aanpak
De beste manier om de pijpleiding is om eerst een stuk langs het strand aan te leggen en dan recht door zee naar het boorplatform. Om de goedkoopste oplossing te bepalen moeten we de totale kosten minimaliseren. Noem de totale kosten van het aanleggen K miljoen euro. De kosten voor het aanleggen langs het strand noemen we S miljoen euro per kilometer, door zee Z. De afstand (in km) van het boorplatform tot het strand noemen we y, die van het beginpunt tot het boorplatform d, en die van het beginpunt tot het punt op het strand recht tegenover het boorplatform x. De lengte van de pijpleiding langs het strand noemen we a en die door zee noemen we b.
Er geldt dus dat
K = a S + b Z.
en met de stelling van Pythagoras (sqrt = wortel)
b = sqrt(y^2 + (x - a)^2).
Dus de totale kosten zijn
K = a S + sqrt(y^2 + (x - a)^2) Z.
De minmimale kosten kun je vinden door K te differentieren naar a en gelijk aan nul te stellen. Dat geeft
S + (x - a) / (sqrt(y^2 + (x-a)^2) * Z = 0.
Werken we de bovenstaande vergelijking verder uit dan vinden we
(x - a)^2 = S^2 y^2 / (Z^2 - S^2).
a = x - S y / sqrt(Z^2 - S^2) (hier gebruiken we dat Z groter is dan S).
Nu kunnen we het resultaat voor a invullen in de eerste formule. We vinden dan dat de minimale kosten gelijk zijn aan
K = x S + y * sqrt(Z^2 - S^2).
Nu is x gelijk aan 8 km (sqrt(10*10 - 6*6)), y gelijk aan 6 km, S is 0,3 miljoen euro per km, en Z is 0,5 miljoen euro per kilometer. Vullen we alles in dan vinden we dat K = 2,4 + 2,4 = 4,8 miljoen euro.
Het aanleggen van de pijpleiding op de goedkoopste manier kost dus 4,8 miljoen euro.
De natuurkundige aanpak
Voor het probleem van het boorplatform is een ook een veel eenvoudiger oplossing. Tenminste, als je de stap durft wagen om het vraagstuk om te zetten in een natuurkundig probleem.
We veranderen ÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂgeldÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂ in ÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂtijdsduurÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂ en passen het probleem aan. Het gaat er nu om de afstand tussen A en B in zo weinig mogelijk tijd af te leggen. Langs het strand gaat met 0,3 s per km (snelheid v1 = 3,33 km/s), door zee gaat het met 0,5 s per km (snelheid v2 = 2 km/s). En wat is nu meer geschikt op dit vraagstuk op te lossen dan een lichtstraal (die immers altijd de kortste weg in tijd kiest)? Zie hier onder een schets van de situatie.

De straal gaat van A naar C en wordt gebroken naar B. Bij C is de invalshoek i = 90 graden, de brekingshoek is r. Volgens de brekingswet van Snellius is:
sin 90/sin r = v1/v2, dus: sin r = v2/v1 = 0,6.
Dan moet r = 36,9 graden en dus tan r = 0,75.
Dan volgt: CD = 4,5 km en AC = 3,5 km (want AD = 8 km). Verder is CB = 7,5 km.
De tijd voor AC is dus 3,5 x 0,3 = 1,05 s; de tijd voor CB is 7,5 x 0,5 = 3,75 s.
Totaal is dat 4,8 s.
Nu volgt de ÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂterugvertalingÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂ naar miljoenen euroÃÂÃÂÃÂÃÂÃÂÃÂÃÂÃÂs.
|
|