De ommuurde tuin II - reken rdzl
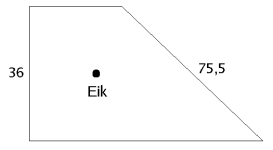
| Een tuin wordt omgeven door vier muren, die een rechthoekig trapezium vormen. De tegenover elkaar liggende zijden (die niet evenwijdig zijn) hebben lengtes van 36 en 75,5. In het midden van de tuin staat een markante eik. De eigenaar merkt op dat deze eik precies gelijke afstanden heeft tot elk van de vier muren die de tuin omsluiten. Hoeveel is de oppervlakte van de tuin? |
|
Uitleg
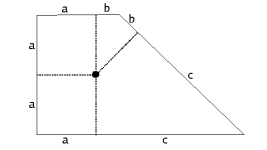
| De eik vormt het midden van een cirkel (met straal a = 18) die precies aan alle muren raakt. De evenwijdige zijden zijn samen: 2a + b + c, en dat is dus gelijk aan 36 + 75,5 = 111,5. Dus de oppervlakte bedraagt de som van de twee evenwijdige zijden maal de halve hoogte, dus: 111,5 x 18 = 2007. |
|
|
|