Beurskoersen voorspellen - reken rdzl
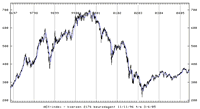
| Wat is de kans dat de koers van een willekeurig gekozen aandeel dat op de euronext beurs te Amsterdam wordt verhandeld, begint met het cijfer 1? |
|
Uitleg
Op het eerste gezicht lijkt het juiste antwoord misschien wat vreemd, de kans de koers van een willekeurig gekozen aandeel met het cijfer 1 begint is namelijk ongeveer 30% en niet zoals je misschien zou verwachten 1/9 = 11%.
Bij beurskoersen kun je aannemen dat hoge koersen (1000 euro per aandeel) minder vaak voorkomen dan lage koersen (1 euro per aandeel). Maar er zijn natuurlijk ongeveer evenveel aandelen die een koers tussen de 9 en 10 euro hebben als die een koers tussen de 10 en de 11 euro hebben. Dus aangenomen dat de koers 19 euro maar een klein beetje minder vaak voorkomt dan 10 euro kun je zeggen dat de kans dat een koers tussen de 10 en de 19 euro ligt iets minder dan 10 keer de kans is dat de koers tussen de 9 en 10 euro ligt. Hetzelfde geldt natuurlijk voor hogere koersen, de kans dat een koers tussen de 100 en 199 euro ligt is ongeveer 10 keer de kans dat de koers tussen de 90 en 99 euro ligt. Omdat hoge koersen minder vaak voorkomen, betekent dit dat de kans dat de koers met het cijfer 1 begint ongeveer 10 keer de kans is dat het cijfer 9 begint. Koersen die met het cijfer 1 beginnen zullen dus relatief vaak voorkomen.
Nu een wat wiskundiger uitleg met de berekening. Noem de waarschijnlijkheidsdichtheidsfunctie voor beurskoersen P(x). (x is een bedrag in euro's). Dit betekent dat de kans dat een beurskoers tussen x1 en x2 ligt gelijk is aan

Natuurlijk geldt dat
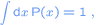
oftewel de totale kans is gelijk aan 1. Als men de beurskoersen in dollars (y) zou uitdrukken is de waarschijnlijkheidsdichteidsfunctie in dollars P(y) = P(k*x), waarbij een dollar is gelijk aan k euro's. Er geldt dat

oftewel de kans dat een beurskoers tussen de 1 en 2 dollar zit is gelijk aan een constante keer de kans dat de koers tussen de 1 en 2 euro ligt. De kansverdeling is

Dus

Door de vergelijking P(k*x) = 1/k P(x) naar k te differentiÃÂÃÂÃÂÃÂÃÂÃÂÃÂëren en k gelijk aan 1 te stellen kan men afleiden dat x P'(x) = -P(x). Hieruit volgt dat P(x) = c/x. c is een constante die bepaald kan worden door de kansverdeling te normeren op 1.
Met deze waarschijnlijkheidsdichtheidsfunctie kunnen we uitrekenen wat de kans is dat een koers met het cijfer B begint. Die is dan
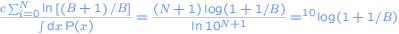
Bij beurskoersen kun je aannemen dat hoge koersen (1000 euro per aandeel) minder vaak voorkomen dan lage koersen (1 euro per aandeel). Maar er zijn natuurlijk ongeveer evenveel aandelen die een koers tussen de 9 en 10 euro hebben als die een koers tussen de 10 en de 11 euro hebben. Dus aangenomen dat de koers 19 euro maar een klein beetje minder vaak voorkomt dan 10 euro kun je zeggen dat de kans dat een koers tussen de 10 en de 19 euro ligt iets minder dan 10 keer de kans is dat de koers tussen de 9 en 10 euro ligt. Hetzelfde geldt natuurlijk voor hogere koersen, de kans dat een koers tussen de 100 en 199 euro ligt is ongeveer 10 keer de kans dat de koers tussen de 90 en 99 euro ligt. Omdat hoge koersen minder vaak voorkomen, betekent dit dat de kans dat de koers met het cijfer 1 begint ongeveer 10 keer de kans is dat het cijfer 9 begint. Koersen die met het cijfer 1 beginnen zullen dus relatief vaak voorkomen.
Nu een wat wiskundiger uitleg met de berekening. Noem de waarschijnlijkheidsdichtheidsfunctie voor beurskoersen P(x). (x is een bedrag in euro's). Dit betekent dat de kans dat een beurskoers tussen x1 en x2 ligt gelijk is aan

Natuurlijk geldt dat
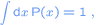
oftewel de totale kans is gelijk aan 1. Als men de beurskoersen in dollars (y) zou uitdrukken is de waarschijnlijkheidsdichteidsfunctie in dollars P(y) = P(k*x), waarbij een dollar is gelijk aan k euro's. Er geldt dat

oftewel de kans dat een beurskoers tussen de 1 en 2 dollar zit is gelijk aan een constante keer de kans dat de koers tussen de 1 en 2 euro ligt. De kansverdeling is

Dus

Door de vergelijking P(k*x) = 1/k P(x) naar k te differentiÃÂÃÂÃÂÃÂÃÂÃÂÃÂëren en k gelijk aan 1 te stellen kan men afleiden dat x P'(x) = -P(x). Hieruit volgt dat P(x) = c/x. c is een constante die bepaald kan worden door de kansverdeling te normeren op 1.
Met deze waarschijnlijkheidsdichtheidsfunctie kunnen we uitrekenen wat de kans is dat een koers met het cijfer B begint. Die is dan
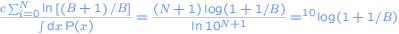
Voor B = 1 krijgen we dan log 2 = 0.3 = 30%. De kans dat een beurskoers met het cijfer 1 begint is dus ongeveer 30%. Dit fenomeen heet de wet van Benford en werkt voor veel meer dingen dan alleen beurskoersen. Bijvoorbeeld met het aantal inwoners van een willekeurig gekozen land of het aantal blaadjes aan een willekeurig gekozen boom in het bos.
Hieronder is een tabel te zien van de de kansen op begincijfers 1 tot en met 9 van de slotkoersen van vrijdag 18 februari 2005.
cijfer kans op cijfer voorspelling 1 0.263682 0.301030 2 0.243781 0.176091 3 0.139303 0.124939 4 0.089552 0.096910 5 0.129353 0.079181 6 0.049751 0.066947 7 0.014925 0.057992 8 0.059701 0.051153 9 0.009950 0.045757
Duidelijk te zien is dat de kans op het begincijfer 1 veel groter is dan op de andere begincijfers en dat deze kans ongeveer 30% is.
|
|