Appel - reken rdzl
| Karel heeft een perfect bolvormige appel. Met een appelboor drukt hij het klokhuis er uit. Er blijft zo een cilindervormig gat over waarvan het midden precies door het midden van de appel gaat. Karel meet met behulp van een touwtje en een liniaal de lengte van het gat. Het blijkt exact 8 cm te zijn. Wat is nu het volume van de doorboorde appel? |

|
Uitleg
|
Het grappige van dit probleem is dat het niet nodig is om te weten wat de diameter van de appel is om het te kunnen oplossen. Noem de straal van de bol r en die van de appelboor a. De lengte van het gat is 2*d. Zie het plaatje hier rechts, dat een doorsnede is van een deel van de appel. Het volume van de overgebleven appel kan worden gekregen door het volume van het gearceerde deel gedraaid in een cirkel rond de y-as te berekenen. Dat volume V is: 4 * pi * Integraal[tussen x=a en x = r van x * (r^2 - x^2)^(1/2) dx] = 4 * pi (r^2 - a^2)^(3/2) / 3. Nu is gebruikmakend van de stelling van Pytaghoras, a^2 + d^2 = r^2. Als dit resultaat wordt ingevuld in de bovenstaande formule vinden we V = 4 * pi * d^3 / 3. Als het gat een lengte heeft van 8 cm dan is d gelijk aan 4 cm en het volume van de overgebleven appel 268 cm^3. |
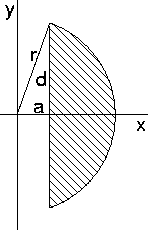
|
|
|